7 Sumber Harmonisa dan Perhitungannya
June 30, 2019
Add Comment
Konverter
Kenyataan menunjukkan, bahwa pemakaian komponen semikonduktor seperti diode dan thyristor dalam konversi energi listrik yang dipakai pada peralatan konverter, inverter dan lain-lainnya serta peralatan elektronika yang dipergunakan untuk mengatur tegangan maupun kecepatan putaran motor menunjukkan makin berkembang pesat pemakainnya.
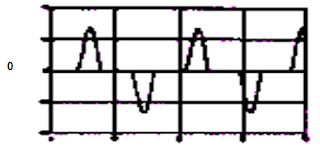
Pemakaian konverter sebagai sumber daya searah membawa kerugian pada jaringan listrik, yaitu merusak bentuk gelombang tegangan dan arus bolak-balik sehingga tidak merupakan gelombang sinusoidal murni. Bentuk gelombang arus dan tegangan yang tidak sinusoidal tersebut mengandung gelombang frekuensi dasar dan frekuensi harmonisa yang dapat menyebabkan adanya gangguan pada sistem tenaga listrik dan sistem lainnya. Berikut ini adalah bentuk-bentuk gelombang harmonik dari berbagai jenis konverter:
Macam-macam sumber harmonik adalah sebagai berikut:
1. Single Phase Power Supply
Type arus distorsinya adalah 80% (high 3rd)
Bentuk gelombang yang dihasilkannya adalah:
2. Semikonverter
Type arus distorsinya high 2nd, 3rd, 4th pada beban parsial.
3. Konverter 6 pulsa dengan smoothing kapasitif tanpa induktor seri
Type arus distorsinya 80%
4. Konverter 6 pulsa dengan smoothing kapasitif dengan induktor seri > 3% atau DC drive.
Type arus distorsinya 40%
5. Konverter 6 pulsa dengan inductor besar untuk smoothing arus.
Type arus distorsinya 28%
6. Konverter 12 pulsa
Type arus distorsinya 40%
7. Regulator Tegangan AC
Type arus distorsinya bervariasi tergantung sudut penyalaannya.
Untuk lebih jelasnya ada beberapa contoh dan penjelasan Sumber-sumber Harmonik.
- Fundamentals of Three-Phase Current Source.
- Conversion Basic (Six-Pulse) Configuration.
- Effect of Transformer Connection.
- Twelve-Pulse Related Harmonics
- Higher-Pulse Configurations
- Effect of Transformer and System Impedance
Perhitungan Tegangan Dan Arus Harmonisa
Metode Fourier Untuk Analisa Harmonisa. Menurut Metode Fourier, suatu fungsi periodik dapat diuraikan menjadi fungsi-fungsi sinusoidal dengan frekuensi, amplitudo dan sudut fasa tertentu asalkan memenuhi syarat-syarat:
- Merupakan fungsi periodik
- f(wt) = f(wt+T) dengan T = periode
- Merupakan fungsi kontinyu atau fungsi tak kontinyu dengan jumlah ketidak kontinyuan yang tertentu selama satu periode
- Selama selang periode, fungsi harus mempunyai harga rata-rata tertentu
- Dalam satu periode T, fungsi harus mempunyai harga maksimum atau minimum yang jumlahnya tertentu.
- Apabila syarat-syarat diatas dipenuhi maka fungsi dapat diuraikan menjadi deret Fourier yang bentuknya sebagai berikut:
- Dengan:
Penyederhanaan analisa Fourier dapat dilakukan dengan menggunakan sifat-sifat khusus sebagai berikut:
- Jika luas siklus positif dan negatif dalam satu periode sama maka a0 = 0.
- Jika f(wt) = -f(wt+p) atau fungsi mempunyai simetri setengah gelombang atau merupakan fungsi ganjil maka tidak akan muncul harmonisa orde genap dan juga an = 0.
- Jika fungsi merupakan fungsi genap f(wt) = f(-wt) maka bn = 0
- Dengan menggunakan Metode Fourier pada bentuk gelombang arus yang diserap oleh komponen atau beban penyebab harmonisa maka dapat ditentukan komponen-komponen harmonisa yang dibangkitkannya. Dan selanjutnya dapat dihitung tingkat tegangan harmonisa pada jaringan.
Kadar Harmonisa yang diijinkan
Karena kehadiran harmonisa pada jaringan sangat mengganggu maka beberapa negara membuat suatu standarisasi tentang berapa kadar harmonisa yang dapat diijinkan terdapat dalam suatu jaringan. Ukuran yang dipakai untuk menyatakan kebesaran harmonisa adalah total distorsi oleh harmonisa (Total Harmonic Distortion), yang disingkat dengan THD, dan didefinisikan sebagai:
THD = (I1/Irms)x100%





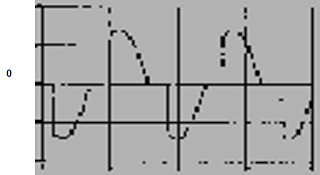
0 Response to "7 Sumber Harmonisa dan Perhitungannya"
Post a Comment